Allocation Doctorale : Simulations HPC de structures

Thématique

Le vieillissement des structures de Génie Civil entraîne d'importants questionnements économiques et écologiques quant au choix entre leur maintenance ou leur remplacement. C'est dans ce contexte que se justifie l'approfondissement des connaissances sur le comportement des matériaux cimentaires, de leurs mécanismes de dégradation à court et long terme ainsi que de leur comportement au sein d'une structure.
Ce domaine scientifique requiert des compétences interdisciplinaires : mécanique des milieux continus non linéaires, comportement des matérieux cimentaires, transferts de masses dans les milieux poreux, calcul numérique à haute performance.

Il est aujourd'hui clairement établi que les mécanismes de dégradation des structures en béton observés à l'échelle macroscopique trouvent leurs origines dans un ensemble de phénomènes physiques et chimiques qui s'opèrent à une échelle plus fine. Leurs conséquences à l'échelle macroscopique sont importantes et ont une influence notable sur la durabilité des structures et donc leur durée de vie.
Ce constat est la pierre angulaire de ce projet qui a pour but de renforcer les liens entre ces échelles.

Domaine

Le cadre du projet est le développement de méthodes numériques permettant de rendre compte du comportement mécanique des matériaux cimentaires en modélisant leur structure à différentes échelles. Les échelles retenues sont:

• Pour l'échelle fine : l'échelle mésoscopique (de l'ordre du mm) pour laquelle sont modélisées les hétérogénéités du matériau (agrégats et macro porosité) ainsi que des éléments d'armatures.
• Pour l'échelle macroscopique : l'échelle de la structure (de l'ordre de quelques décimètres) pour laquelle des sollicitations classiques d'éléments sont modélisées (poutres, poteaux, ...)

La modélisation du comportement mécanique rentre dans le cadre des modèles mésoscopiques [Wriggers, 2006] via l'utilisation d'une méthode Éléments Finis Enrichis adaptés aux matériaux hétérogènes quasi-fragiles [Roubin, 2015a]. Des campagnes expérimentales sous tomographie à RX ont permis de valider la pertinence de ces méthodes [Stamati, 2019] dans un tel cadre. Cependant, les ressources numériques nécessaires aux approches mésoscopiques contraignent les applications à des calculs à l'échelle du matériau.
 

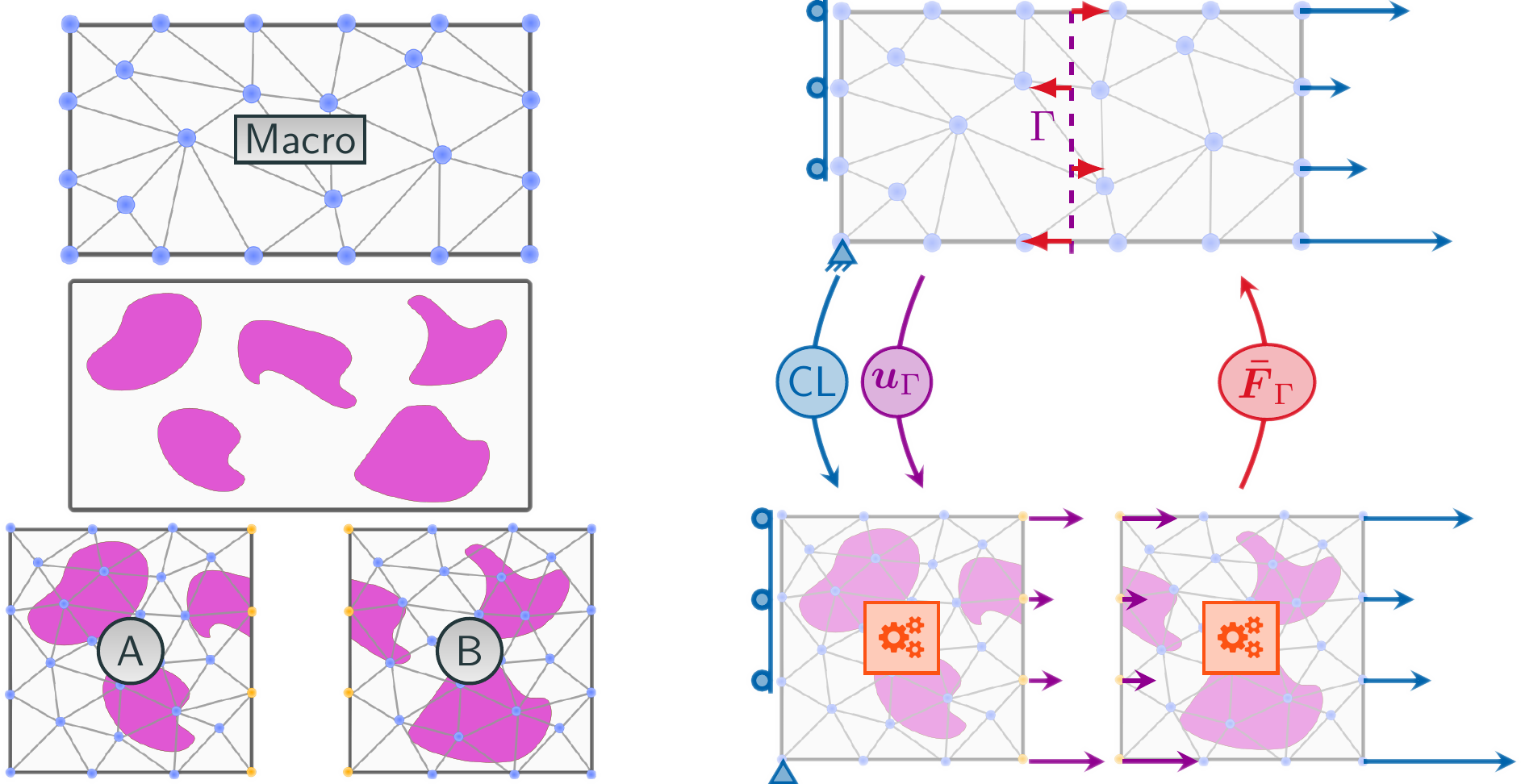
Afin de pouvoir appliquer ce type de modèle à l'échelle de la structure, plusieurs approches sont envisageables :

• Des méthodes de réduction de modèle : le comportement de la mésostructure est projeté sur une base de modes propres obtenus par la POD.
• Des méthodes de couplage fort entre les échelles : le comportement de la mésostructure est homogénéisé numériquement aux points d'intégration du calcul macroscopique (méthode des « éléments finis au carré »).
• Des méthodes de décomposition de domaines : l'échelle macroscopique est « découpée » en plusieurs sous-domaines qui font l'objet de calculs mésoscopiques quasi-indépendants. À l'échelle de la structure, un unique calcul macroscopique grossier est nécessaire, permettant de contrôler les conditions aux limites de chaque calcul fin. Ceux-ci peuvent ainsi être distribués sur des ressources différentes (CPU, RAM).

L'impact de la mésostructure sur le comportement des structures de Génie Civil n'étant pas encore clairement identifié, c'est la méthode de décomposition de domaines qui est retenue dans ce projet. Contrairement aux deux autres approches présentées, elle conserve l'intégralité de la réponse à l'échelle fine au niveau de la structure, ce qui semble pertinent dans le cadre de la modélisation de propagations de fissures. Le développement de ces méthodes sera basé sur des algorithmes éprouvés depuis des décennies dans le cadre de l'élasticité linéaire et l'attention sera particulièrement portée sur le choix des fonctions d'interpolations entre les sous domaines (comme les méthodes « mortiers ») [Wohlmuth, 2001].

Objectifs

L'objectif de ce projet de thèse est de développer des méthodes de décomposition de domaines afin de pouvoir effectuer des calculs mésoscopiques rendant compte explicitement de la mésostructure et des éléments d'armature à l'échelle de la structure.

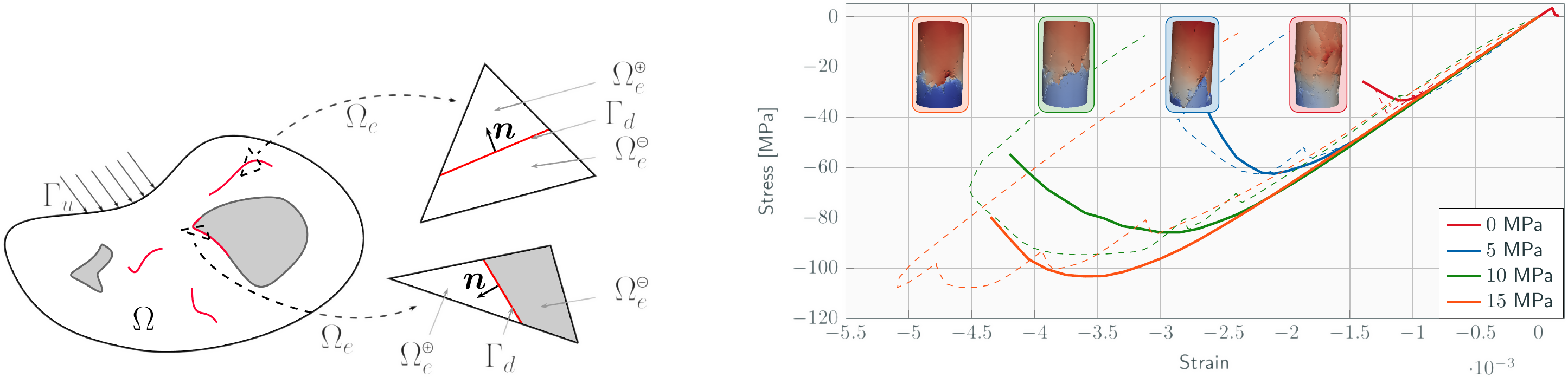
Le premier objectif est de travailler sur un verrou scientifique lié au couplage entre le modèle utilisé et les méthodes de décomposition de domaines. Il n'a pas encore été montré dans la littérature que les modes de rupture des matériaux cimentaires (fissuration), et plus généralement que les comportements non linéaires adoucissants, sont modélisables avec ces méthodes de décomposition. La problématique principale est de réussir à modéliser la propagation des fissures à travers plusieurs sous-domaines, sans modification due à la frontière. Des études préliminaires ont montré des signes prometteurs si les fonctions d'interpolation des problèmes d'interface sont bien choisies (mortiers) [Vallade, 2016].

Le deuxième objectif est d'appliquer ce cadre numérique à des calculs de structure, alliant ainsi, de façon innovante et directe, l'échelle mésoscopique et l'échelle de la structure. Des essais récents effectués sur des nouveaux types de renforts (câbles) pourront être une base de données expérimentales nécessaire à la validation du modèle [Colyvas, 2020].

Contexte

Dans le cadre de l'étude du comportement mécanique des matériaux cimentaires l'échelle mésoscopique porte une quantité importante d'informations liées à sa structure comme la géométrie et la topologie de la morphologie, les propriétés mécaniques de ses phases, les différents mécanismes de fissurations. Les modèles de simulation dits « mésoscopiques » s'intéressent à représenter ces informations aux échelles fines (résolution de l'ordre du millimètre) afin de les prendre en compte explicitement. Ainsi, ces modèles permettent d'adopter une démarche explicative afin d'analyser les conséquences de la mésostructure sur le comportement macroscopique du matériau qui émerge naturellement des simulations.

Les différentes phases matérielles de la mésostructure du matériau étant explicitement représentées (agrégats, porosité, pâte de ciment, ...), la phénoménologie nécessaire pour représenter un comportement donné est donc nécessairement moins complexe que celle employée par des modèles macroscopiques. Cependant, d'un point de vue technique, cet avantage est à mettre en opposition avec la complexité accrue de la méthode de calcul inhérente à la représentation de la mésostructure.

Parmi les problèmes rencontrés par ces approches, ce projet s'intéresse à réduire les coûts des simulations (le coût étant directement lié à la finesse de la discrétisation de la mésostructure) en adoptant des méthodes de décomposition de domaine. De telles approches permettraient, en réalisant des simulations plus performantes, de faire évoluer les problématiques qui peuvent être adressées vers deux échelles opposées : l'échelle de la structure (taille de l'ordre du mètre) et l'échelle microscopique (hétérogénéités de l'ordre du dixième de millimètre).

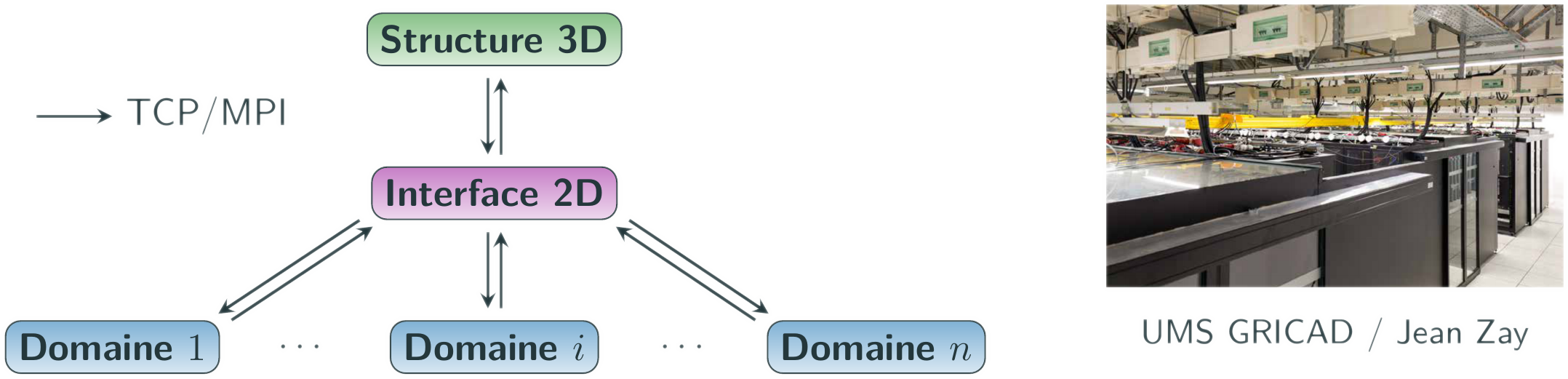
La mise en place de ces méthodes entraînera l'utilisation du supercalculateur régional (UMS Gricad, hébergé par l'UGA), voir national (Jean Zay).

Méthode

Plusieurs choix de méthodes sont nécessaires pour établir le cadre numérique de ce projet: a. le modèle morphologique nécessaire à la représentation des hétérogénéités de la mésostructure b. le modèle mécanique permettant de rendre compte de la fissuration du béton dans un cadre hétérogène c. la méthode de décomposition de domaines permettant d'effectuer les calculs à l'échelle de la structure.

1. Modèle morphologique: le modèle retenu est basé sur le principe d'excursions de champs aléatoires corrélés [Roubin, 2015b]. Il permet en effet de pouvoir assurer des conditions de continuité aux bords des sous domaines et de générer des morphologies aléatoires à plusieurs phases et à formes non idéales (entraînant ainsi des concentrations de contraintes plus réalistes).
2. Modèle mécanique : la méthode des Éléments Finis doublement Enrichis est retenue ici [Roubin, 2015a]. Développée par l'équipe encadrante depuis bientôt 10 ans, les récentes campagnes expérimentales ont montré la pertinence de son utilisation dans le cadre de la fissuration des bétons [Stamati, 2019].
3. Décomposition de domaines : la décomposition de domaines est à voir dans ce projet comme un moyen de communiquer entre l'échelle mésoscopique et l'échelle de la structure . Les différentes méthodes peuvent se regrouper en deux familles : les méthodes séquencés (communication unidirectionnelle de l'échelle macroscopique vers l'échelle fine) et les méthodes intégrées (communication dans les deux sens) [Feyel, 2001]. C'est dans ce dernier cadre que le modèle est utilisé et le raccord entre les est effectué afin d'assurer la continuité des déplacements et des contraintes entre les sous domaines (méthodes hybrides) [Allix et Gosselet, 2020].

Le développement du modèle mécanique a été pensé dans l'optique d'une stratégie multi-échelle et possède les moyens techniques de communication nécessaires à la décomposition de domaines (développement orienté composant, [Kassiotis, 2008]).
En mode de production, ces méthodes nécessitent l'utilisation de supercalculateurs au moins de la taille des supercalculateurs régionaux (politique encouragée par le CNRS) pour pouvoir analyser l'extensibilité des calculs (scalability). L'Université Grenoble Alpes héberge le super calculateur de notre région (Gricad) dont l'accès est ouvert à ce genre de projets académiques. La possibilité de rejoindre le super calculateur national (Jean Zay) géré par la société civile GENCI (Grand Équipement National de Calcul Intensif) est également envisagée.
 

Résulats attendus

• Lever le verrou scientifique relatif à la propagation de fissures macroscopiques en EF et en utilisant une méthode intégrée de décomposition de domaines.
• Appliquer la méthode à des éléments de structure en béton armé, jusqu'à la comparaison avec des essais issus de la littérature.
• Ouvrir des perspectives vers la modélisation mécanique de structures complètes jusqu'à rupture. Avec prise en compte des conditions environnementales (par exemple l'état hydrique). 

Références bibliographiques

1. [Wriggers, 2006] Mesoscale models for concrete: Homogenisation and damage behaviour, Finite Elements in Analysis and Design, 2006.
2. [Roubin, 2015a] Multi-scale failure of heterogeneous materials: A double kinematics enhancement for Embedded Finite Element Method, International Journal of Solids and Structures, 2015.
3. [Stamati, 2019] Tensile failure of micro-concrete: from mechanical tests to FE meso-model with the help of X-ray tomography, Meccanica, 2019.
4. [Wohlmuth, 2001] Discretization Methods and Iterative Solvers Based on Domain Decomposition, Lecture Notes in Computational Science and Engineering, 2001.
5. [Vallade, 2016] Modélisation multi-échelles des shales : influence de la microstructure sur les propriétés macroscopiques et le processus de fracturation, Thèse, 2016.
6. [Colyvas, 2020] Behavior of Reinforced Concrete Beams using Wire Rope as Internal Shear Reinforcement, Engineering, Technology & Applied Science Research, 2020.
7. [Roubin, 2015b] Mesoscale modeling of concrete: A morphological description based on excursion sets of Random Fields, Computational Materials Science, 2015.
8. [Feyel, 2001] Multi-scale non-linear FE2 analysis of composite structures: damage and fiber size effects, 2001, Revue européenne des ÉlémentsFinis : NUMDAM'00.
9. [Allix et Gosselet, 2020] Non intrusive Global/local coupling techniques in solid mechanics:  an introduction to different coupling strategies and acceleration techniques, Modeling in Engineering Using Innovative Numerical Methods for Solids and Fluids, 2020.
10. [Kassiotis, 2008] coFeap's Manual, LMT-Cachan internal, 2008.
11. [Stamati, 2020] SPAM: Software for Practical Analysis of Materials, Journal of Open Source Software, 2020.