Thèse de Donatien Rossat

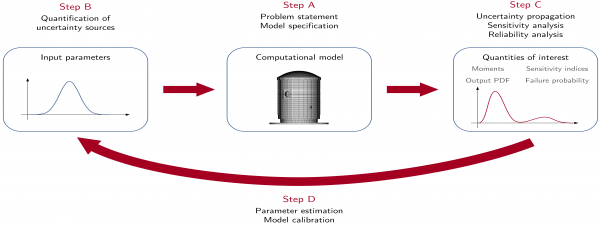
This work falls within the context of the aging of large concrete containment structures, such as reactor buildings in nuclear power plants. It aims at devising a numerical strategy for forecasting the long-term physical behavior of such structures, in order to better anticipate their maintenance.

Recent improvements of the understanding of physical phenomena behind aging and the increase of computational resources have enabled the development of numerical models aiming at simulating the Thermo-Hydro-Mechanical and Leakage (THML) behavior of large aging concrete structures. Nevertheless, the input parameters of such models are tainted with uncertainties, due to a lack of knowledge or to a natural randomness. Consequently, this thesis is mainly based on the general framework of Uncertainty Quantification (UQ), aiming at explicitly modeling uncertainties in numerical simulation. In this framework, the uncertainties tainting input parameters are typically modeled by probability laws, and are subsequently propagated through the model in order to study the variability of its response, or to estimate specific quantities of interest, such as moments or quantiles. However, THML computational models typically involve a large amount of uncertain parameters, most of them being not measurable directly. For this reason, the input probability law modeling their uncertainties is usually chosen in a subjective way, based on expert judgement. Then, this thesis is placed in the framework of Bayesian inference, in order to update a prior level of knowledge on input parameters from noisy observational data of the response of the structure under study.

Firstly, this work aims at coupling Bayesian inference with numerical techniques adapted with THML computational models, these last most often lying on costly finite element codes. In this perspective, a recent Bayesian computational framework is studied as an alternative to classical MCMC sampling techniques, and a coupling with surrogate modeling techniques is proposed in order to efficiently draw samples from posterior distributions with a reduced computational cost. Next, a general methodology aiming at performing probabilistic forecasts of the long-term THML behavior of containment structures is presented. In this context, the uncertainties of input parameters of the adopted THML model are quantified through Bayesian inference, from in-situ monitoring data. The proposed methodology is illustrated through a study of the VeRCoRs mock-up (1:3 scale nuclear containment building).

Lastly, in the framework of a reliability analysis, this thesis aims at estimating risks of exceeding regulatory leakage thresholds, while modeling the effect of eventual maintenance operations. In this framework, the impact of the choice of the inputs' probability law on some quantity of interest (including probabilities of failure) is assessed, through a robustness analysis. Next, a Bayesian approach aiming at updating both probabilities of failure and input parameters from monitoring data is presented. The overall methodology is applied to the realistic case of an operating 1:1 scale nuclear containment building.

Jury