- Imprimer
- Partager
- Partager sur Facebook
- Partager sur X
- Partager sur LinkedIn
Soutenance
Le 9 novembre 2023
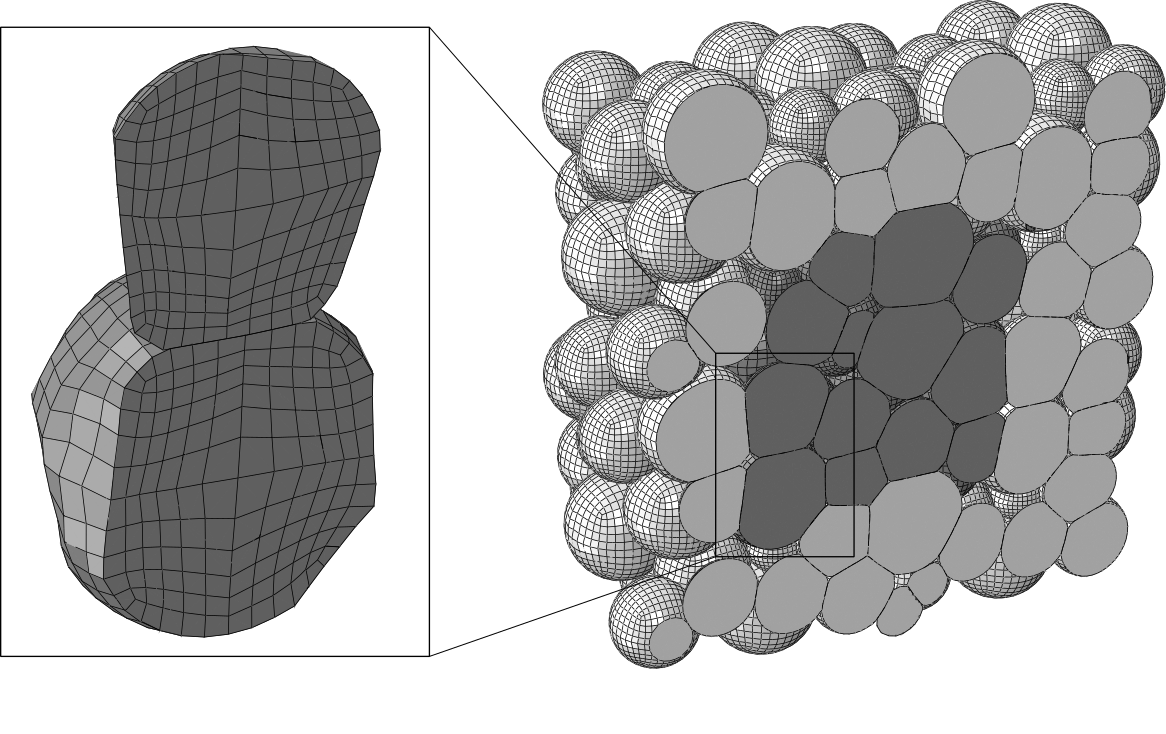
Micromechanical modelling of the densification of a cohesive granular medium made up of ductile particles
The cold compaction process of powders made up of ductile particles is widely used in the industry. During this forming phase, interparticle adhesion develops during densification, building up the mechanical strength of the manufactured parts. One of the main challenges of this process is the occasional occurence of failure during densification, due to highly deviatoric stresses in the vicinity of geometric singularities. These defects lead to the rejection of the manufactured parts. Despite widespread recognition of this problem, there are few studies in the literature focusing on the micro-mechanical understanding of these failure phenomena within this type of material involving highly deformable particles. Currently, there is no numerical model capable of predicting the formation of such defects. Only time-consuming trial-and-error procedures efficiently mitigate them. Given the often expensive and challenging nature of experimental campaigns along complex loading paths, the role of particle adhesion and deformability in rupture phenomena remains poorly understood.
Given these limitations, a numerical approach based on the multi-particle finite element method appears as a promising alternative. Such a method allows for the explicit modelling of the microstructure of an idealized granular medium, considered as a representative assembly of particles. The method corresponds to a coupling between the finite element method and the discrete element method\!: the particles are meshed in volume so as to fully account for their deformations through constitutive laws based on continuum mechanics; and the interactions between particle surfaces are handled using finite-element contact formulations. The main drawback of this method lies in its high computational cost, limiting the number of particles that can be modelled. However, by employing a multi-scale approach, it is possible to derive mesoscopic mechanical properties associated with an equivalent Cauchy volume element from the simulation of a relatively small number of particles, through homogenization techniques and formulation of appropriate boundary conditions. A study focusing on the analysis of the influence of boundary conditions on the simulated mechanical response of a numerical granular sample subjected to quasi-static loading is thus proposed.
Such a micro-mechanical approach requires an accurate description of contact interactions. Specifically, the mechanical strength of parts obtained through powder compression is significantly influenced by the development of adhesion at the contact level. Therefore, a multi-scale adhesive contact model, based on the weighting of the surface energy by a roughness model, is implemented in the multi-particle finite element code. This contact model allows for the local prediction (at each node of the finite element mesh) of the level of adhesion developed by external mechanical loads, which is consistent with the powder compaction process. The constructed numerical model is finally used to predict the mesoscopic properties associated with the equivalent Cauchy volume element. This numerical model enables the exploration of highly deviated loading paths that are inaccessible experimentally. Its purpose is to support the future development of continuum mechanics-based model for the modeling of a powder volume during compression.
Jury
Mme Emmanuelle VIDAL-SALLÉ - professor, INSA Lyon (Reviewer)
Mr Émilien AZÉMA - professor, Université de Montpellier (Examiner)
Mr Christian GEINDREAU - professor, Université Grenoble Alpes (Examiner)
Mr Didier IMBAULT - assistant professor, Grenoble INP (PdD Supervisor)
Mr Barthélémy HARTHONG - assistant professor, Grenoble INP (Co-PdD Supervisor, guest)
Date
Jeudi 09 novembre 2023 13h30
Localisation
Amphithéatre Kilian (1381 rue de la piscine, 38610 Gières)




- Imprimer
- Partager
- Partager sur Facebook
- Partager sur X
- Partager sur LinkedIn