Sols, solides, structures, risques

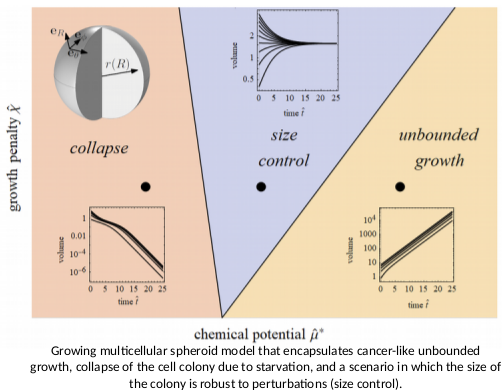
The mechanism with which cells measure the dimension of the organ in which they are embedded, and slow down their growth when the final size is reached, is a long-standing problem in developmental biology. Feedback loops between growth and mechanical stress are increasingly believed to be important. In this presentation, I will introduce the concept of morphoelasticity as a standard continuum framework for modelling growing elastic tissues and provide insight into the feedback loops between growth and stress by considering simple 1D and 2D examples, such as a spring growing against a passive medium. However, without additional variables, the classical morphoelasticity theory often leads to either a collapse or unbounded growth of the tissue and prohibits reaching a finite asymptotic size. To address this issue, I will show how to modify the classical setting by including an energetic cost associated with growth, leading to the physical effect of size control.

These ideas will be applied to a specific system of a multicellular spheroid growing against the pressure of a medium in which it is embedded. The present model provides a qualitatively correct residual stress profile and has a naturally emerging necrotic core, both of which have been established experimentally in multicellular spheroids, and could be a step towards a better understanding of the role of mechanics in growing biological tissues.