- Imprimer
- Partager
- Partager sur Facebook
- Partager sur X
- Partager sur LinkedIn
Séminaire
Le 28 octobre 2021
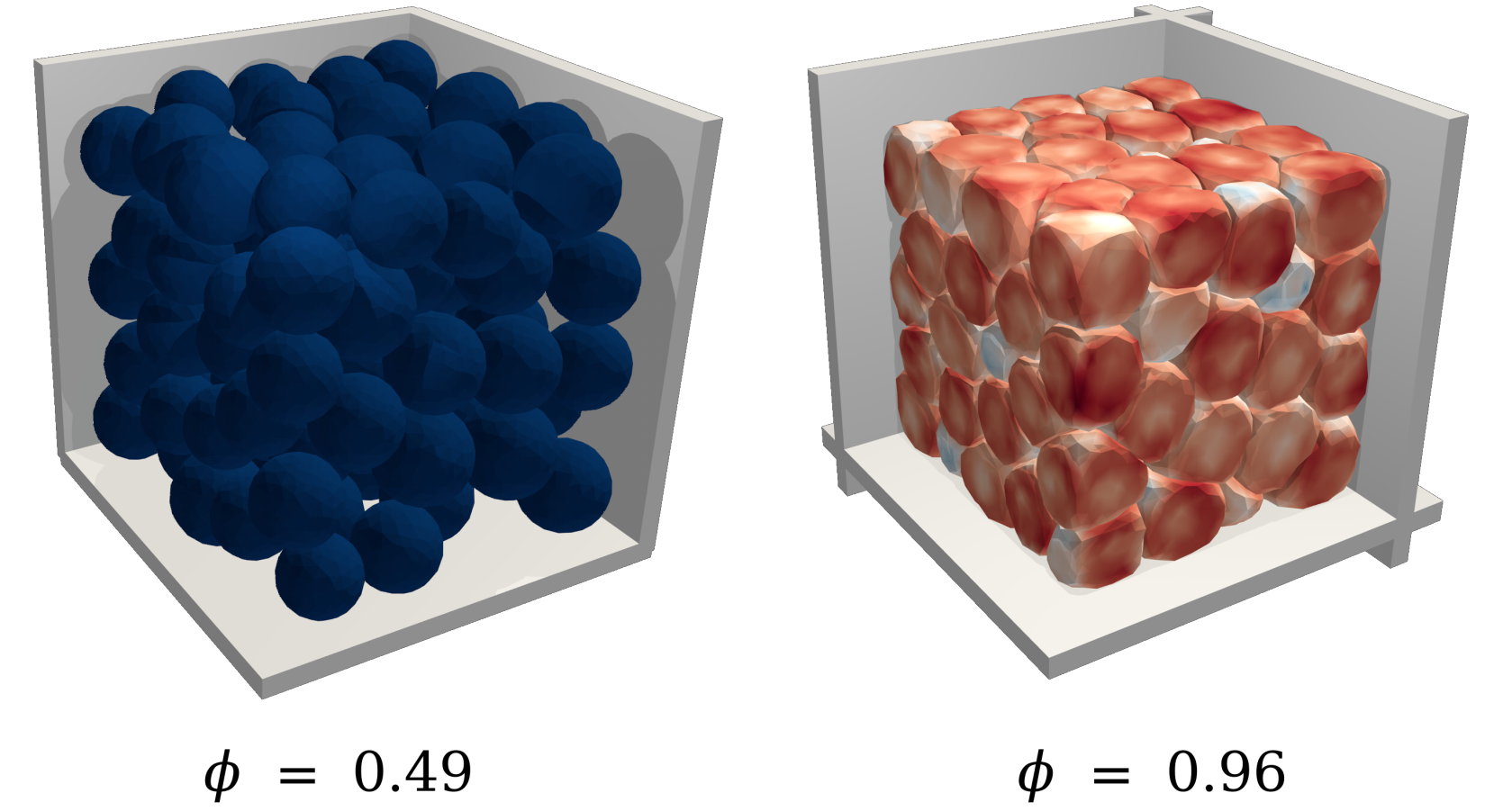
Compaction of soft granular packings.
The compaction behavior of deformable grain assemblies beyond jamming remains misunderstood, and existing models that seek to find the relationship between the confining pressure P and solid fraction ϕ end up settling for empirical strategies or fitting parameters. Numerically and experimentally, we analyze the compaction of highly deformable frictional grains of different shapes and soft/rigid particle mixtures in two and three dimensions: numerically, using a coupled discrete - finite element method, the Non-Smooth Contact Dynamics Method (NSCD), and experimentally using high-resolution imaging coupled with a dedicated DIC algorithm. We characterize the evolution of the packing fraction, the elastic modulus, and the microstructure (particle rearrangement, connectivity, contact force, and particle stress distributions) as a function of the applied stresses. We show that the solid fraction evolves non-linearly from the jamming point and asymptotically tends to a maximal packing fraction, depending on the soft/rigid mixture ratio, the friction coefficient, and the particle shape. At the microscopic scale, different power-law relations are evidenced between the local grain structure and contacts, and the packing fraction and pressure, regardless of the shape, the mixture ratio, or the dimensionality (2D/3D). A significant outcome of this work is the development of a theoretical and micromechanical-based approach for the compaction of soft granular assemblies far beyond the jamming point. This latter is derived from the granular stress tensor, its limit to small deformations, and the evolution of the connectivity. Furthermore, from the expression of these well-defined quantities, we establish different compaction equations, free of ad hoc parameters, well-fitting our numerical and experimental data. These equations mainly depend on the dimensionality, where the characteristics of shape, elastic bi-dispersity, and compression geometry (uniaxial vs isotropic) are considered as input parameters. Our theoretical framework allows us to unify the compaction behavior of assemblies of soft, soft/rigid, and noncircular soft particles coherently, both in 2D and 3D, for isotropic and uniaxial compression.
Date
14h00
Localisation
Bâtiment Galilée Salle 011
Download the slides
- Imprimer
- Partager
- Partager sur Facebook
- Partager sur X
- Partager sur LinkedIn