- Share
- Share on Facebook
- Share on X
- Share on LinkedIn
Séminaire
On February 2, 2024
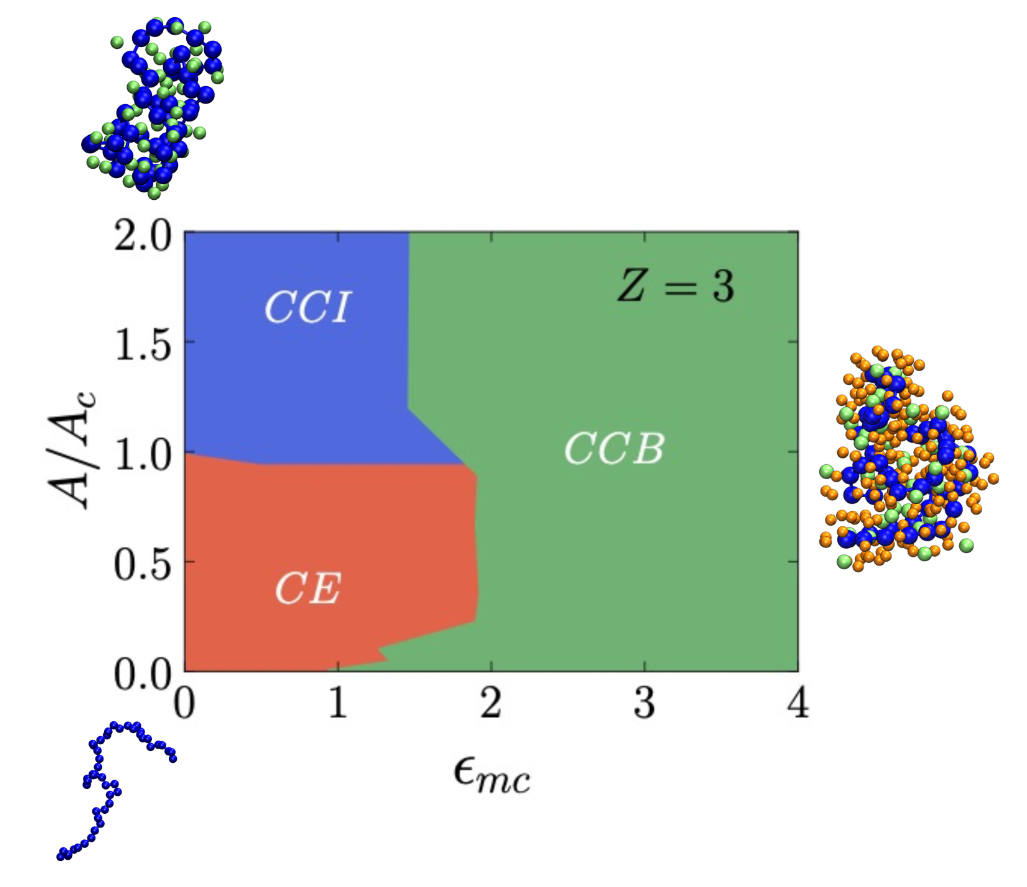
The conformational phase diagram of charged polymers in the presence of attractive bridging crowders
Charged polymers or polyelectrolytes (PEs) are ubiquitous. The conformations
of highly charged PEs are influenced by a combination of factors, including
long-range electrostatic interactions, solvent quality, temperature, counterion
valency, and dielect ric constant of the solvent. In this seminar, we will discuss
the impact of attractive neutral crowders on the conformations of a single,
similarly charged PE in the presence of oppositely charged counterions. Us-
ing extensive molecular dynamics simulations utilizing generic coarse-grained
bead–spring models, we identify three distinct phases: (1) the CCI phase
(Charged Collapsed due to Intra-polymer interactions), which corresponds to a
collapsed state primarily driven by the condensation of counterions; (2) the CE
phase (Charged Extended), characterized by an extended conformation of the
polymer due to repulsive electrostatic interactions within the PE; and (3) the
CCB phase (Charged Collapsed due to Bridging interactions), representing a
secondary collapsed state primarily induced by the presence of attractive bridg-
ing crowders, with a substantial number of crowders located within the col-
lapsed conformation. By identifying the phase transitions among these phases,
we obtain the phase diagram in the PE charge density and polymer–crowder
interaction phase space for monovalent, divalent, and trivalent counterions. Our simulations reveal that the interaction with
crowders can induce collapse, despite the presence of strong repulsive electrostatic interactions, and can replace condensed coun-
terions to facilitate a direct transition from the CCI and CE phases to the CCB phase.
Date
10h30
Localisation
Galilée room 015
- Share
- Share on Facebook
- Share on X
- Share on LinkedIn