- Share
- Share on Facebook
- Share on X
- Share on LinkedIn
Soutenance
On September 3, 2021
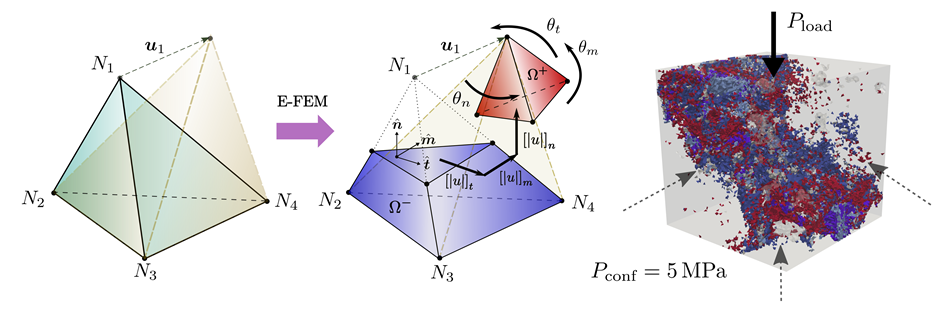
An E-FEM generalisation for the modelling of triaxial fracture processes in composite quasi-brittle materials on the mesoscale
Representation of an element local fracture using the Embedded Finite Element Method approach (left and centre). The element is internally segmented in two different bodies possessing a set of fracture kinematic modes, where only translational and rotational are currently shown for the sake of clarity. In the right, the resulting local fracture networks in a concrete cubic sample simulation subject to a confinement pressure of 5 MPa and a progressive compressive load attaining a fully developed fracture process. Elements in a blue colour palette present a mode I local failure type while elements in a red colour palette exhibit a mode II failure mode with local sliding kinematics. Elements in purple have failed under compaction considerations.
Jury
Yann MALECOT Professeur des universités, Université Grenoble Alpes,Directeur de thèse
Jean-Baptiste COLLIAT Professeur des universités, Université de Lille, Rapporteur
Delphine BRANCHERIE Maître de conférences, Université de Technologie Compiègne, Rapporteure
Delphine BRANCHERIE Maître de conférences, Université de Technologie Compiègne, Rapporteure
Nicolas MOËS Professeur des universités, École Centrale de Nantes, Examinateur
Bert SLUYS Professeur des universités, Delft University of Technology, Examinateur
Loredana CONTRAFATTO Professeur associé, Catania University, Examinatrice
Gioacchino VIGGIANI Professeur des universités, Université Grenoble Alpes, Examinateur
Codirection :
Laurent DAUDEVILLE
Bert SLUYS Professeur des universités, Delft University of Technology, Examinateur
Loredana CONTRAFATTO Professeur associé, Catania University, Examinatrice
Gioacchino VIGGIANI Professeur des universités, Université Grenoble Alpes, Examinateur
Codirection :
Laurent DAUDEVILLE
Professeur des universités, Université Grenoble Alpes, Codirecteur de thèse
Emmanuel ROUBIN
Maître de conférences, Université Grenoble Alpes, Co-encadrant de thèse
Maître de conférences, Université Grenoble Alpes, Co-encadrant de thèse
Date
On September 3, 2021
Complément date
9h30
Localisation
Complément lieu
- Amphi Kilian Campus Gières (limited to 40 registered persons)
- Remote live session

- Share
- Share on Facebook
- Share on X
- Share on LinkedIn